The experimental derivation of p-y curves follows a traditional process of double derivation and double integration of pile curvature data measured through internal instrumentation. Most commonly, strain gauges, LVDT’s and inclinometers are used to obtain pile curvature readings over the various levels of lateral pile deformation. Once curvature data are recorded, the deflections, rotations, and bending moments in the pile are calculated through the beam bending equation using finite difference or finite element numerical techniques. Hereby, most studies assume that the axial load in the pile, Q, has very little effect on the deflection and bending moment and is assumed constant with depth.
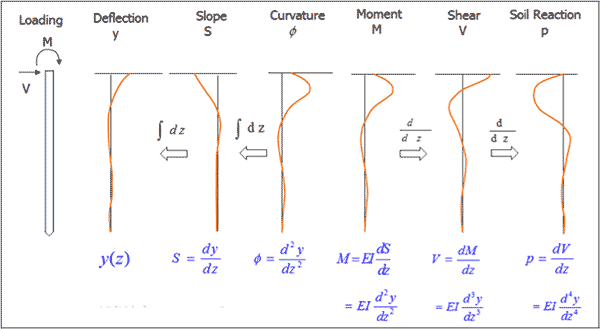
In order to derive the analytical, closed form solution for the mathematical description of p-y curves, additional boundary conditions are necessary to balance the number of equations and the number of unknowns. Two boundary conditions at the pile top and two at the bottom of the pile are most commonly assumed:
AT THE BOTTOM OF THE PILE:
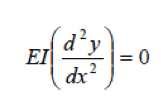
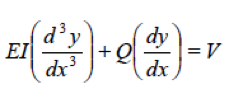
AT THE TOP OF THE PILE:
The two boundary conditions at the top of the pile depend on the shear, moment, rotation, and displacement circumstances at the top of the pile.